Organizing Scrapwork with Flowcharts

A question came up recently on a GMAT forum:

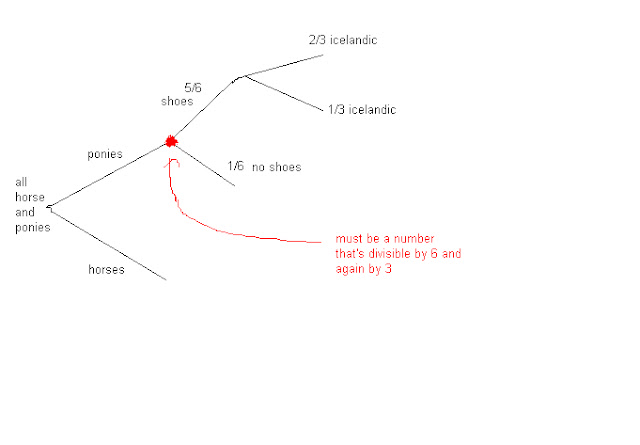
"A ranch has both horses and ponies. Exactly 5/6 of the ponies have horsehoes, and 2/3 of the ponies with horseshoes are Icelandic. If there are 3 more horses than ponies, what is the minimum number of horses and ponies combined on the ranch?"

A question like this can be tough to conceptualize, but sometimes a picture really is worth 1000 words. So here is a visual aid that you can use to understand questions like this in the future:

I hope this helps a little. Organizing it this way, you can see that the number of ponies must be a number divisible by 6 and again by 3 -- in other words, a number you can divide by 6 and then take that result and divide it by 3. So the minimum number would be 18. Then if there are 3 more horses than ponies, there must be 21 horses. That makes the minimum number of horses/ponies to be 39 total.

If you don't see why the number of horses must be divisible by 6 and then by 3, just try inserting a number that's not divisible by 6 into that place in the flowchart and you'll see that you end up with non integer values for the horses and ponies. You can't have half a pony any more than you can have half a bunny! :)

Do you run on autopilot?

Quick brainteaser for you: If 3 bunnies can eat 3 carrots in one hour, how many carrots can 1.5 bunnies eat in one hour?

Really take a moment to think about it.

Do you have an answer?

Ok. If you answered, or even were tempted to answer, “1.5 carrots,” then I’m glad that you’re reading this article! The thing is, while the bunnies are eating carrots at the rate of one per hour, it doesn’t follow that 1.5 bunnies will eat 1.5 carrots. 1.5 bunnies will only eat one carrot, because 1.5 bunnies is really just 1 bunny. (That half a bunny isn’t feeling very well and doesn’t want any carrots.)

I don’t mean to say that this is a GMAT-style problem, but if you found yourself answering “1.5 carrots,” then you are prone to operating on autopilot. Students who operate on autopilot will often fall into traps, and they may become overwhelmed by questions that don’t fall clearly into easily recognized patterns. And let me tell you – you will likely see many problems on the GMAT that don’t fall into common patterns!

It’s imperative that you understand the role that active thinking plays in GMAT success. Sometimes I tell my students, “The GMAT is a math test the way that hockey is an ice skating contest.” They usually look at me like I’m crazy until I explain, so let me explain. Of course all hockey players can skate. They can skate backwards, forwards, sideways…. They can stop on a dime and accelerate just as easily. But they’re playing hockey while they’re doing all of that, right? They watch the puck, they shoot the puck, they defend their goal and attack the other goal. I’m not a hockey expert, but it seems to me that skating skills aren’t nearly enough. Hockey requires that you skate expertly, and yet it isn’t exactly an ice skating contest.

And that’s my entire point. The GMAT isn’t a math test, exactly. It assumes you can do math. It assumes you can solve for x in your sleep. It assumes that you can tick off the major exponent rules on your fingers and reverse-FOIL without taking a breath. But… then what? It’s not enough that you can do the math – you also have to do the thinking. A lot of students just work automatically through GMAT problems. But that’s not enough.

The GMAT often gives you questions that test your ability to think creatively. For example, consider this problem. (It’s based off of a real Official Guide question.)

A café sells cupcakes for $1.00 each and donuts for $1.30 each. If a customer buys some cupcakes and some donuts for a total of 13.10, how many cupcakes did the customer buy?

A)    4

B)     5

C)    6

D)    7

E)     8

Take a moment to see if you can solve the problem.

Really, try!

Did you give it a try? Ok.

A lot of students would begin working here on autopilot. Did you? The “automatic” response would be to write something like 1C + 1.1D = 13.10. Sure, there’s nothing particularly wrong with that. It’s a true representation of the mathematical relationship here. Unfortunately, it doesn’t help us solve the problem.

No one can actually use the equation C + 1.1D = 13.10 to solve for C or D. There are infinite solutions to that problem, if it’s looked at solely algebraically. You would need either another equation or the value of D in order to find C. Then how can this be solved?

The question makes it clear that there is only one solution, so there must be only one way that  $1 cupcakes and $1.30 donuts can add up to $13.10. The trick is to focus on the .10 part from the 13.10. How can we ensure that the sum ends in 10 cents? 

The cupcakes cost exactly $1 each, so it isn’t the cupcakes’ fault that the price includes ten cents. So, it must be that the price of the donuts ends in 10 cents. One donut would cost 1.30, two would cost 2.60, three would cost 3.90, four would cost 5.20, six would cost 6.50, seven would cost 7.80, and eight would cost 9.10. So it must be that the person bough eight donuts, so that the price would end in 10 cents. It’s the only way that it would end in 10 cents (knowing that the sum is only 13.10). Then we would just need enough cupcakes to bring the total to 13.10, so we’d need four cupcakes. The customer must have bought 4 cupcakes.

As you can see, this problem depended as much on your logic skills and focus as it did on your math skills. And that’s exactly my point. By all means, study your math skills. They’re foundational. But as you work through each problem, stay engaged and focused. Thinking – active, creative, and purposeful thinking – is just as necessary for success on the GMAT as strong math skills are. All the algebra drills in the world won’t tell you when not to use algebra, and no perfectly constructed proportion can explain why 1.5 bunnies can’t eat 1.5 carrots.

So, try this tonight. Try a practice set of quant questions, preferably from the Official Guide to GMAT review, with the goal of staying fully engaged. Begin each problem by keeping your hands behind your back for ten seconds while you think through the problem fully and make sure that you’re not operating on autopilot.

I never would have thought of that.....

Have you ever found yourself saying, when you heard or read the explanation to a problem, “I never would have thought of that?” Ultimately, this will do nothing but undermine your success.

Let’s unpack what it means when students say this self-defeating mantra, and why it’s so important to stop saying it!

Assumption #1: Because I didn’t come up with it myself, I never will be able to do it.

A lot of the time, students expect themselves to be able to invent solving methodologies themselves. “I never would have thought of that,” they sigh, and what they mean is: “What is wrong with me that I didn’t think of it myself? The fact that I didn’t think of it myself is all the proof I need that this test is beyond me.”

I was talking about this phenomenon with a friend of mine who also tutors for the GMAT, and he just laughed and said, “I never would have thought of the Pythagorean Theorem on my own! I don’t know why students often seem unhappy to learn from the past.”

Think about it though: Nearly everything you know how to do is something that someone taught you to do. Your parents taught you how to brush your teeth and tie your shoes. Your teachers taught you science and foreign languages and all sorts of other topics. From books you may have learned to cook or trade on the stock market, and friends may have taught you fashion tips or how to play poker. You didn’t invent any of these skills from scratch. You learned these things. That’s what humans do – we learn from earlier generations. (That’s why we have such a lengthy maturation process, compared to other species.)

Don’t beat yourself up because you don’t invent your own methods for solving data sufficiency or critical reasoning problems. If a teacher or a book shows you a new method, focus on how much it will help you next time, instead of focusing on the fact that you didn’t know it before.

Assumption #2: Other people can do that because they’re inherently better at the test than I am.

Sometimes when a student says, “I never would have thought of that,” they sort of smile as if that’s a compliment to me. In this case, “I never would have thought of that” sort of implies that the only reason that I, Laura, thought of it is that I have some sort of intrinsic ability that the student lacks. But that’s just not the case!

I wasn’t born on this Earth knowing how to do the GMAT. In fact, when I was younger, I got pretty bad grades in math. I just hated it! I learned how to do math as an adult and found that when I had the right mindset, I could succeed at it in a way that I had never been able to when I was a teenager.

The reason that I often have an intuitive or quick solution to tough problems is that I have learned a lot about math and verbal content. I’ve also learned how to approach word problems when I get stuck, and how to take methodical steps through strange and confusing data sufficiency problems. I’ve learned when it’s worth it to spend an extra moment or two checking my work, and I’ve learned when it’s time to cut and run. You can learn these things too.

In other words: people who are good at the GMAT don’t necessarily have some sort of inborn and unattainable talent that other people don’t have. Skill depends on practice and honest reflective assessment of your performance. Knowledge comes from study. And scores come from skill and knowledge.

Don’t stand under a flag that says, “I’m not one of those people who are good at the GMAT.” There’s no such thing as “those people,” and you can be whoever you want to be.

Assumption #3: That isn’t the way I think, so I’m going to stick with the method I’m used to.

A while back I was working with a tutoring student on a problem that required her to multiply 54 by 17 and then divide by 27. She diligently multiplied out 54 x 17, and then set up the long division to divide the result by 27. I asked her to wait for a moment, and re-wrote the problem as a fraction:

(54)(17)
    27

I asked her if she saw a shortcut, and she said that she didn’t. I suggested that something might reduce, and the second I said the word “reduce” the student immediately saw that 54 could cancel with the 27:

(54)2(17)    =    (2)(17) =     34
    27                      1  

She looked at what she had done, how quickly she had solved the problem with the help of that shortcut, and sighed and said, “I never would have thought of that.” And by that she meant: “I never will think of that in the future. That isn’t the way my mind works. So there’s no point in trying to learn.”

She absolutely knew how reduce. Her arithmetic skills were very sharp! However, she didn’t look for opportunities to reduce. I suggested to her that she make an effort in the future to remember to look for opportunities to use her excellent skills with reducing in fractions, so that she could perform her calculations more quickly and easily.

At first, though, she really didn’t believe that she ever would recognize an opportunity to reduce. “I’ve been doing it the long way forever,” she said. “It’s just how I think.” Her argument was that since she was never going to learn how to do it the faster way, she’d have to just stick with the way she was comfortable with – even though it hadn’t been getting her the scores she wanted and even though it was actually harder and slower than the fast way. I finally helped her see that saying “it’s just how I think” was really just an excuse to not try something new.

We finally decided that the student should write “reduce!” at the top of each page of her scrap paper when she worked on quant. She made it her goal of the week to find opportunities to reduce. It wasn’t easy for her at first, but after a while it got to be more natural. These days she’s reducing like a pro and her pacing has improved a great deal in quant. I’m sure she can barely remember the day that she said that she’d never learn to reduce.

You’re not so set in your ways that you can’t learn something new. If you ever catch yourself thinking, “I would never have thought of that, so that’s not the right method for me,” ask yourself: Is this method really too hard for you? Or have you decided that good enough is good enough for you? While it’s true that some methods are better than others for some people, don’t rule out a method completely just because it isn’t your initial instinct.

Assumption #4: If it doesn’t come easily to me, then it means that there is something wrong with me and I’ll never get better at this.

In this case, “I never would have thought of that” means something a lot closer to “I give up.” I’ve seen students say “I never would have thought of that” while they lean back sadly in the chair and sigh.

I know that studying for the GMAT can be exhausting and sometimes even a little depressing. But nothing worth having is easy, and the work you put into the GMAT absolutely will be worth it down the road. It doesn’t come easy to most people. The difference is that some people keep working through it until it gets easier.

There’s nothing wrong with you if you find the GMAT tough. Don’t give up just because it doesn’t come to you quickly. A friend of mine used to say, “The only difference between success and failure is one more try,” and while I think that’s almost intolerably cheesy, I also think it’s true.

So:
Next time you find yourself saying “I never would have thought of that,” stop yourself and say, “But next time, I WILL.”